While in an office supplies store I saw a display rack full of "Singing Candles" and thought it would be interesting to take one apart to see how it works.
I've already taken off the white end cap when I took the picture.
There's a pre-made hole in the candle through which the thin silver strip threads and out the top of the candle.
The MCU is in the black glob of course. The red ceramic capacitor is 10nF. The negative terminal of the button battery is soldered to the pcb.
An S9014 NPN transistor drives the speaker. Base current limiting resistor is 4.7K 1/4-watt.
This is the speaker.
Other end of the speaker. It doesn't show in the pics but there's a coil of enamel wire if you peer into the holes.
Tinned pcb tracks after the retaining clip, rectangular metal bridge and metalized strip have been removed
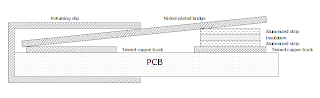
From left to right: retaining clip, rectangular metal bridge, metalized strip, pcb
The narrow silver strip consists of two electrically conductive
metalized outer layers and a nonconducting layer sandwiched in between. Measured resistance at DMM probe-to-probe distance of 1cm is 9 ohms, and ~60 ohms at 7 cm.
The following is a stylized diagram showing how the strip is positioned on the pcb tracks. Thickness of the strip and tracks are exaggerated of course just for illustration purposes.
The rectangular nickel-plated bridge sits on top of the strip and one of the tinned pcb tracks, providing an electrical pathway from the top layer of the strip to the other track. However, because of the insulating layer, the track on which the strip rests is isolated from the other track. A retaining clip secures the bridge and strip to the pcb.
As you might have seen in the first couple of images above the blister pack has a "press here"
sticker that allows the would-be buyer to test the candle before
purchasing. After opening the package I took a look at what they had
under the sticker and found there's a 1-cm diameter aluminum foil
glued beneath the plastic film and another on the cardboard. Ohmmeter check confirms they're zero ohm. There's one or
two millimeters of airspace between the top and bottom foil. When the user pushes down
on the plastic film the two foils make contact. At the same time they pinch the exposed silver
strip. This causes electrical contact between the two outer layers of
the strip and immediately wakes
up the MCU thus causing the music to start playing. Only a momentary contact is necessary and the MCU will play the song three times.
Here's the musical candle in action.
Here's what I think happens: When the candle is lit and the flame begins to burn the strip, carbon forms and provides a relatively low resistance between the metalized layers, thus causing a switching action which wakes the MCU up (via an interrupt-on-change of sorts). As long as the candle is lit the MCU plays the song over and over.
Interestingly when the flame is snuffed out the MCU stops playing (not immediately but only after playing the song three in a row after the last check of the pin monitoring the "strip switch"). This implies that the resistance of the carbon and other substances in the burnt strip markedly increases when it cools down. Reigniting the wick quickly brings the temperature back up and causes the resistance to decrease once again thus triggering the MCU.
Pics of strip after candle had been lit
Wednesday, June 27, 2012
Monday, June 25, 2012
Measuring liquified petroleum gas (LPG) levels
Before anything else, I forgot to mention in in the LPG detection test that I took temperature measurements of the TGS2610 sensor of the LPM2610 module using a Fluke 87V and its thermocouple. After the module had been powered up for many minutes I held the thermocouple junction to the case for a couple of minutes and obtained a maximum reading of 52.8°C. Ambient temperature was 32.7°C. I am not confident with this case temperature measurement. Contact area between thermocouple and case is small and manually holding the thermocouple did not of course properly secure it to the sensor. Taping or even gluing it in place may be a more reliable way of taking a measurement.
As I mentioned in Detecting LPG, it occurred to me that we can use the Figaro LPM2610 module to not just detect the presence of LPG when it's >= 10% of its lower explosive limit (LEL), we may also be able to use its analog outputs to measure the amount of gas in the air.
Before we jump in, a couple of caveats relevant to measuring gas levels. The TGS2610 datasheet says the sensor's typical detection range is between 500 to 10,000 ppm. Given butane LEL = 18,000 ppm, the sensor's detection range translates to 2.8% to 55.5% LEL. I want to be able to measure all the way down to 1% but it looks like this may be asking too much from this sensor. Then again we can take our chances.
Secondly, the sensor is hardly accurate as can be seen in this Figaro diagram of the module's expected performance:
The note below the chart says
Given these characteristics, using the LPM2610 to measure gas levels seems almost foolhardy. But in quixotic fashion we shall nevertheless proceed--if only as a mathematical exercise.
To start off here's a list of definitions of terms and variables we'll be using:
![V_{OUT(act)} = \left [\frac{R_{L}}{R_{L}+R_{S(act)}}\right ] V_{DD}](http://latex.codecogs.com/gif.latex?V_%7BOUT%28act%29%7D%20=%20%5Cleft%20[%5Cfrac%7BR_%7BL%7D%7D%7BR_%7BL%7D+R_%7BS%28act%29%7D%7D%5Cright%20]%20V_%7BDD%7D)
Given our definitions of standard sensor resistance and output voltage it follows that:
![V_{OUT(std)} = \left [\frac{R_{L}}{R_{L}+R_{S(std)}}\right ] V_{DD}](http://latex.codecogs.com/gif.latex?V_%7BOUT%28std%29%7D%20=%20%5Cleft%20[%5Cfrac%7BR_%7BL%7D%7D%7BR_%7BL%7D+R_%7BS%28std%29%7D%7D%5Cright%20]%20V_%7BDD%7D)
The LPM2610 module is calibrated at an ambient temperature of 20°C where VREF = VDD/2. As ambient temperature deviates from 20°C, VREF is adjusted by the module's thermistor. In our equations we will need to determine VOUT(std). And so we need to adjust VOUT(act) by a certain factor. This correction factor is as follows:
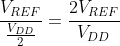
To transform that table of data into a formula we perform regression analysis. If we plot the above we end up with a nonlinear curve, one which shows the characteristics of a power law curve where y = axb. Unfortunately, the spreadsheet I'm using can only do linear regression. Fortunately, we can work around this limitation. If we plot the values in the above table on a log-log paper (where x and y axes are graduated in a logarithmic scale), we get a nearly straight line and not a curve. Therefore, we can take the log(x) and log(y) and plug those in the linear regression equations. Solving for the log of both x and y, i.e., of %LEL and RS(std), we obtain the following:
We let the spreadsheet perform a linear regression using the above logarithmic data and it magically spews out the following:
b = x coefficient = -0.471269891979091
c = constant = 3.91103846203761
r squared = 0.999483957661255
r2 is the square of the correlation coefficient. Since it's practically = 1 it implies that the correlation between data and the equation is extremely high. Keeping in mind that we had used the logarithms of x and y, the regression equation is:
log(y) = b*log(x) + c
Here's a plot of both the datasheet values (red points) and computed line using an online linear regression calculator:
Taking the antilog of both sides of the equation above gives us:
y = 10[b*log(x) + c]
Table below shows the computed RS(std) and the %error from values given in the datasheet.
Recall that I performed a linear regression because my spreadsheet does not have the capability of doing a power regression. However, there are various online resources that we can use, obviating the need to get the logarithms of x and y. Plugging the data from the very first table above into a power regression calculator gives us the following results:
a = 8147.7643914991
b = -0.471269892
correlation coefficient = 0.9998059883
So the power equation is
y = 8147.7643914991x-0.471269892
Now, since both the linear and power equations yield the same y we can equate the two:
axb = 10[b*log(x) + c]
Taking the log of both sides we obtain:
log(a) + b*log(x) = b*log(x) + c
log(a) = c
Indeed, if we take the log of 8147.76 we get 3.911
Bear in mind that the above equations apply only to TGS2610 ID#15. Nevertheless, upon subjecting ID#10 and #20 to power regression and computing for VOUT(std) as a percentage of VDD I obtained results which confirmed the guess that they'd all show practically the same characteristic voltage outputs given their respective voltage divider resistor values. Click the "Vout as %Vdd" tab at the bottom of the following spreadsheet to see the computed values. Take a look at the columns with blue headers. The percentages for each of the three ID# are practically the same for every %LEL.
There's at least two ways--when using a microcontroller--to determine the % LEL: direct computation and use of a look-up table.
Given the voltage divider in the TGS2610 sensor and from our definition of standard values we infer that:
![V_{OUT(std)} = \left [\frac{R_{L}}{R_{L}+R_{S(std)}}\right ] V_{DD}](http://latex.codecogs.com/gif.latex?V_%7BOUT%28std%29%7D%20=%20%5Cleft%20[%5Cfrac%7BR_%7BL%7D%7D%7BR_%7BL%7D+R_%7BS%28std%29%7D%7D%5Cright%20]%20V_%7BDD%7D)
From the above power regression we have:
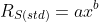
Therefore:
![V_{OUT(std)} = \left [\frac{R_{L}}{R_{L}+ax^{b}}\right ] V_{DD}](http://latex.codecogs.com/gif.latex?V_%7BOUT%28std%29%7D%20=%20%5Cleft%20[%5Cfrac%7BR_%7BL%7D%7D%7BR_%7BL%7D+ax%5E%7Bb%7D%7D%5Cright%20]%20V_%7BDD%7D)
Given VOUT(act) we can obtain VOUT(std) by applying the corrective factor:
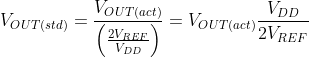
Rearranging the terms, substituting and solving for x:
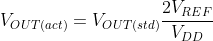
![V_{OUT(act)} = \left [\frac{R_{L}}{R_{L}+ax^{b}}V_{DD} \right ]\frac{2V_{REF}}{V_{DD}}](http://latex.codecogs.com/gif.latex?V_%7BOUT%28act%29%7D%20=%20%5Cleft%20[%5Cfrac%7BR_%7BL%7D%7D%7BR_%7BL%7D+ax%5E%7Bb%7D%7DV_%7BDD%7D%20%5Cright%20]%5Cfrac%7B2V_%7BREF%7D%7D%7BV_%7BDD%7D%7D)
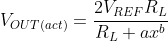
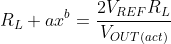
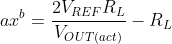
![x^{b} = \left [ \frac{R_{L}}{a} \right ] \left [\frac{2V_{REF}}{V_{OUT(act)}} - 1 \right ]](http://latex.codecogs.com/gif.latex?x%5E%7Bb%7D%20=%20%5Cleft%20[%20%5Cfrac%7BR_%7BL%7D%7D%7Ba%7D%20%5Cright%20]%20%5Cleft%20[%5Cfrac%7B2V_%7BREF%7D%7D%7BV_%7BOUT%28act%29%7D%7D%20-%201%20%5Cright%20])
![x = \sqrt[b]{\left [ \frac{R_{L}}{a} \right ] \left [\frac{2V_{REF}}{V_{OUT(act)}} - 1 \right ]}](http://latex.codecogs.com/gif.latex?x%20=%20%5Csqrt[b]%7B%5Cleft%20[%20%5Cfrac%7BR_%7BL%7D%7D%7Ba%7D%20%5Cright%20]%20%5Cleft%20[%5Cfrac%7B2V_%7BREF%7D%7D%7BV_%7BOUT%28act%29%7D%7D%20-%201%20%5Cright%20]%7D)
RL is a constant and will be contingent upon the particular TGS2610 unit being used (its ID# will determine what RLwill be).
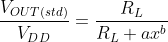
As we already obtained in the direct computation method:
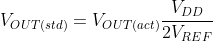
We then divide VOUT(std) by VDD to obtain a unitless fraction:
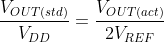
So all the MCU has to do is evaluate the relatively simply equation on the right and then look for the closest value in the table to determine %LEL.
As I mentioned in Detecting LPG, it occurred to me that we can use the Figaro LPM2610 module to not just detect the presence of LPG when it's >= 10% of its lower explosive limit (LEL), we may also be able to use its analog outputs to measure the amount of gas in the air.
Before we jump in, a couple of caveats relevant to measuring gas levels. The TGS2610 datasheet says the sensor's typical detection range is between 500 to 10,000 ppm. Given butane LEL = 18,000 ppm, the sensor's detection range translates to 2.8% to 55.5% LEL. I want to be able to measure all the way down to 1% but it looks like this may be asking too much from this sensor. Then again we can take our chances.
Secondly, the sensor is hardly accurate as can be seen in this Figaro diagram of the module's expected performance:
The note below the chart says
When using LPM2610, typical alarm tolerances for 10% LEL of LP gas such as those shown in the figure above can be expected. However, in actual usage, alarm thresholds may vary since the threshold is also affected by such factors as the tolerances of test conditions and heat generation inside the gas detection enclosure.The tolerances are pretty wide: 5 to 20% LEL. Not at all encouraging.
Given these characteristics, using the LPM2610 to measure gas levels seems almost foolhardy. But in quixotic fashion we shall nevertheless proceed--if only as a mathematical exercise.
To start off here's a list of definitions of terms and variables we'll be using:
- Standard values are sensor resistance and output voltage at an ambient temperature of 20°C. To standardize a voltage is to apply a corrective factor provided by VREF so that the voltage value becomes that which would be expected if ambient = 20°C.
- Actual values are LPM2610 resistance and output voltage values without consideration to ambient temperature.
- VREF is the output of the LPM2610 voltage divider consisting of a thermistor and various fixed-value resistors. VREF is theoretically = VDD/2 when ambient temperature = 20°C.
- VOUT(act) = actual output of the LPM2610 voltage divider consisting of (1) the TGS2610 sensor whose resistance varies with amount of LPG present and (2) a fixed value load resistor RL.
- RS(act) = actual sensor resistance in the LPM2610
- RS(std) = standard sensor resistance
- VOUT(std) = standard voltage output given RS(std)
- RL = load resistance in series with RS
Preliminary equations
Take a look at the LPM2610 circuit diagram above. Given the voltage divider RS and RL, output voltage VOUT is given by the equation below. VOUT in this case is the actual VOUT and RS is the actual RS.Given our definitions of standard sensor resistance and output voltage it follows that:
The LPM2610 module is calibrated at an ambient temperature of 20°C where VREF = VDD/2. As ambient temperature deviates from 20°C, VREF is adjusted by the module's thermistor. In our equations we will need to determine VOUT(std). And so we need to adjust VOUT(act) by a certain factor. This correction factor is as follows:
Derivation of RS(std) Equation
We need to find an equation that describes sensor resistance in terms of % LEL. Since Figaro provides no equation we need to derive it from sensor data. Fortunately, Application Note for LP Gas Detectors using TGS2610 lists RL = RS for various %LEL and TGS2610 ID numbers (ID# corresponds to specific sensor resistances). For example the Figaro LPM2610 modules that I got have sensors with ID#15. From the AN here are its characteristics:| % LEL | RS(std) in ohms |
|---|---|
| 5 | 3830 |
| 10 | 2740 |
| 15 | 2260 |
| 20 | 2000 |
To transform that table of data into a formula we perform regression analysis. If we plot the above we end up with a nonlinear curve, one which shows the characteristics of a power law curve where y = axb. Unfortunately, the spreadsheet I'm using can only do linear regression. Fortunately, we can work around this limitation. If we plot the values in the above table on a log-log paper (where x and y axes are graduated in a logarithmic scale), we get a nearly straight line and not a curve. Therefore, we can take the log(x) and log(y) and plug those in the linear regression equations. Solving for the log of both x and y, i.e., of %LEL and RS(std), we obtain the following:
| log(%LEL) | log(RS(std)) |
|---|---|
| 0.698970004336019 | 3.58319877396862 |
| 1 | 3.43775056282039 |
| 1.17609125905568 | 3.3541084391474 |
| 1.30102999566398 | 3.30102999566398 |
We let the spreadsheet perform a linear regression using the above logarithmic data and it magically spews out the following:
b = x coefficient = -0.471269891979091
c = constant = 3.91103846203761
r squared = 0.999483957661255
r2 is the square of the correlation coefficient. Since it's practically = 1 it implies that the correlation between data and the equation is extremely high. Keeping in mind that we had used the logarithms of x and y, the regression equation is:
log(y) = b*log(x) + c
Here's a plot of both the datasheet values (red points) and computed line using an online linear regression calculator:
Taking the antilog of both sides of the equation above gives us:
y = 10[b*log(x) + c]
Table below shows the computed RS(std) and the %error from values given in the datasheet.
| % LEL | RS(std) in ohms | error in % |
|---|---|---|
| 5 | 3816 | -0.36 |
| 10 | 2753 | 0.47 |
| 15 | 2274 | 0.62 |
| 20 | 1986 | -0.72 |
Recall that I performed a linear regression because my spreadsheet does not have the capability of doing a power regression. However, there are various online resources that we can use, obviating the need to get the logarithms of x and y. Plugging the data from the very first table above into a power regression calculator gives us the following results:
a = 8147.7643914991
b = -0.471269892
correlation coefficient = 0.9998059883
So the power equation is
y = 8147.7643914991x-0.471269892
Now, since both the linear and power equations yield the same y we can equate the two:
axb = 10[b*log(x) + c]
Taking the log of both sides we obtain:
log(a) + b*log(x) = b*log(x) + c
log(a) = c
Indeed, if we take the log of 8147.76 we get 3.911
Bear in mind that the above equations apply only to TGS2610 ID#15. Nevertheless, upon subjecting ID#10 and #20 to power regression and computing for VOUT(std) as a percentage of VDD I obtained results which confirmed the guess that they'd all show practically the same characteristic voltage outputs given their respective voltage divider resistor values. Click the "Vout as %Vdd" tab at the bottom of the following spreadsheet to see the computed values. Take a look at the columns with blue headers. The percentages for each of the three ID# are practically the same for every %LEL.
Determining % LEL
There's at least two ways--when using a microcontroller--to determine the % LEL: direct computation and use of a look-up table.
I. Direct Computation
The direct way is to derive a formula which the microcontroller can use to calculate the amount of gas detected (as % LEL).Given the voltage divider in the TGS2610 sensor and from our definition of standard values we infer that:
From the above power regression we have:
Therefore:
Given VOUT(act) we can obtain VOUT(std) by applying the corrective factor:
Rearranging the terms, substituting and solving for x:
RL is a constant and will be contingent upon the particular TGS2610 unit being used (its ID# will determine what RLwill be).
II. Look-up Table
The other method--which is less CPU intensive--would be to compare the standardized VOUT as a fraction of VDD with the values in a look-up table to determine % LEL (eg., to the nearest %). The look-up table is populated with values computed using the following formula, where x = %LEL and a and b derived from power regression:As we already obtained in the direct computation method:
We then divide VOUT(std) by VDD to obtain a unitless fraction:
So all the MCU has to do is evaluate the relatively simply equation on the right and then look for the closest value in the table to determine %LEL.
Monday, June 18, 2012
June 6, 2012 Venus transit pics
Another off topic entry. Should've uploaded these images on the day I took them. Transit began about an hour after sunrise and ended noon. It was a depressingly cloudy day and I had to keep monitoring the skies and took pics whenever there was a break. Never actually had absolutely clear skies--haze and high altitude cirrus clouds were practically a fixture. The first five images below were obviously taken even with clouds in the way (you hear Joni Mitchell singing Both Sides Now?). Well, at least I got something. It is a once-in-a-lifetime event, you know.
Camera used was an el cheapo Canon Powershot A480 point and shoot. I used one green-tinted welding goggle glass pane during the first couple of hours but doubled it by around 9am. I just held the glass in front of the lens. Camera was for most part mounted on a tripod. ISO rating was initially set to 80 but in most of the shots it was in auto. Maximum optical + digital zoom using spot metering with the sun centered in the metering zone. Bracketing was performed throughout the shoot--I incremented/decremented exposure compensation by one notch (1/3 stop). Shot some 250 frames, 80% of which are either severely overexposed or underexposed, blurry from camera shake (two welding glass plates is so effective in limiting sunlight that shutter speed went as low as 1/60 sec), lack of focus or hazy due to cloud cover. Venus of course crossed the sun in a straight line but because I moved the camera the planet seems to be all over the place.
Camera used was an el cheapo Canon Powershot A480 point and shoot. I used one green-tinted welding goggle glass pane during the first couple of hours but doubled it by around 9am. I just held the glass in front of the lens. Camera was for most part mounted on a tripod. ISO rating was initially set to 80 but in most of the shots it was in auto. Maximum optical + digital zoom using spot metering with the sun centered in the metering zone. Bracketing was performed throughout the shoot--I incremented/decremented exposure compensation by one notch (1/3 stop). Shot some 250 frames, 80% of which are either severely overexposed or underexposed, blurry from camera shake (two welding glass plates is so effective in limiting sunlight that shutter speed went as low as 1/60 sec), lack of focus or hazy due to cloud cover. Venus of course crossed the sun in a straight line but because I moved the camera the planet seems to be all over the place.
Sunday, June 17, 2012
Braking distance and time on level road and on an incline
Off topic entry. Nothing to do with electronics. But I've been obsessed with (or should I say possessed by) this topic for the past week or so. Just want to have all the equations and derivations in one place so I can refresh my memory if I need to in the future.
Let
vi = initial velocity, m/s
vf = final velocity, m/s
v = average velocity, m/s
a = deceleration rate, m/s2
t = time to stop the vehicle, s
d = braking distance, m
μ = coefficient of friction, unitless
Ff = force of friction, kg·m/s2
Fn = normal force (force perpendicular to surface), kg·m/s2
Fg = force due gravity pulling the vehicle down a slope, kg·m/s2
m = mass, kg
g = gravitational acceleration, 9.8 m/s2
θ = angle of inclination (positive if vehicle going uphill, negative if going downhill)
Final velocity is given by the equation:
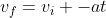
If vf = 0 then
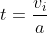
Distance is given by:
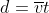
Average velocity is:
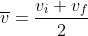
Given vf = 0 and substituting we have:
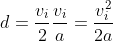
Alternatively we can derive the distance formula using kinetic energy and work equations:
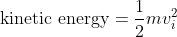
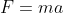
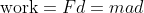
Equating work and energy we have:
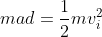
Solving for d we obtain:
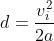
The force of friction is given by the following formula:
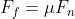
If the vehicle is on a level surface then normal force is just its weight. Therefore,
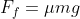
Since
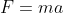
then
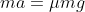
Therefore,
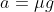
Substituting the above into the distance and time equations we get:
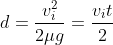
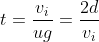
Interesting to note that we can (at least in principle) determine the coefficient of friction by noting the velocity when the brakes are fully applied and time to bring the vehicle to a dead stop.
Now let's tackle the situation when the vehicle is braking on a slope.
When the vehicle is on an incline then a portion of the gravitational force acts to pull the vehicle down the slope. This force we denote as Fg and is derived via basic vector analysis. Refer to the free-body diagram. On the left of the diagram is an object on an incline with an angle of θ. Its weight is labeled as mg. Normal force Fn is the component of mg that is perpendicular to the incline. Fg is the component of mg that is parallel to the incline. To the right I've drawn a vector addition of the forces. Since this is a right triangle we can use the pertinent trigonometric functions: Sin θ = opposite side / hypotenuse. Cos θ = adjacent side / hypotenuse. Since the hypotenuse = mg we obtain the following:
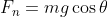
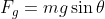
An aside: Since the above are the legs of the right triangle it follows from the Pythagorean theorem that
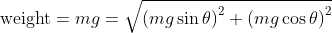
When on a slope with the brakes engaged so that the vehicle is at a standstill Ff is the force that keeps the vehicle from slipping and sliding down and acts in the opposite direction as Fg which is pulling it down the incline. The net force holding the vehicle in place is therefore Ff - Fg. It stands to reason that when Fg becomes >= Ff then the vehicle--even with the brake pads fully gripping the brake discs and drums--will begin to slip and slide. We can calculate the angle of inclination at which this will occur:
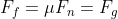
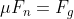
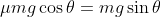
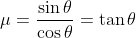
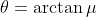
Bear in mind that in this case we are using the static coefficient of friction rather than kinetic (or sliding) coefficient of friction since the vehicle is at rest with respect to the road.
When a vehicle is going downhill its braking distance will increase because a fraction of the gravitational force is acting to pull it down even when the brakes are applied. θ will be negative if going downhill, and so Fg will be negative. When going uphill part of gravitational force adds to the force of friction thereby decreasing braking distance.
The sum of forces acting on the vehicle parallel to its direction of motion is given by:
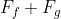
Since
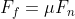
Therefore,
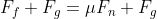
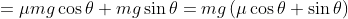
Since
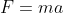
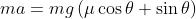
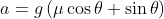
Substituting into our distance and time equations we obtain:
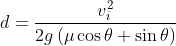
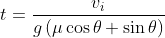
The above are exact equations in contrast to the approximate formula using road grade. The gradient is equal to the rise over run, or tangent of θ. The arctangent of the gradient = angle θ.
Reminder: when using the above equations θ should be negative when the vehicle is going downhill. Given -90° < θ < 0, sin θ is negative while cos θ is positive. Hence Fg is effectively subtracted from Ff. When going uphill and θ is positive then Ff is effectively increased by amount Fg. As anyone who's driven knows, it's harder to bring a vehicle to a stop when going downhill. And that it's easier to do so when going uphill than when on a level road.
Beware that the above distances and times do not take into account the driver's perception and reaction time--the time to perceive the need to stop and the time to actually to apply the brakes. This takes a minimum of around half a second for a driver who's alert and concentrating on the road, but may be much greater if the driver is drowsy, tired, intoxicated, on his cell phone, has poor eyesight, etc. or if visibility is poor among other possible factors beyond the driver's control.
The distance traveled by the vehicle during this time is simply
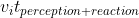
Here are a couple of online braking distance calculators which don't, however, have provisions for vehicles on an incline:
http://www.csgnetwork.com/stopdistcalc.html
http://forensicdynamics.com/stopping-distance-calculator
Tables of coefficients of friction:
http://www.engineeringtoolbox.com/friction-coefficients-d_778.html
http://www.roymech.co.uk/Useful_Tables/Tribology/co_of_frict.htm
Summary of the relevant data from the above tables:
A point worth mentioning: While the wheels are turning static coefficient of friction is operative because at the point of contact the tire is not sliding along the road. This is desirable because the static coefficient is higher than the kinetic coefficient of friction thus leading to decreased braking distance. Anti-lock brakes (ABS) prevent the wheels from locking even when the driver slams the brake pedal, therefore preventing the tires from skidding and sliding. However, the speed of the tire is lower than the vehicle's and so some slip occurs between tire and road. The static coefficient of friction cannot therefore be applied to vehicles even if they're equipped with ABS. For safety reasons it's best to be conservative and use the kinetic coefficient.
The take home lessons from the above formulas:
Braking distance varies with the square of velocity. Thus, doubling one's speed quadruples the distance. Increasing one's speed from 40kph to 100kph increases the braking distance by (100/40)2 = 6.25 times. Braking time, on the other hand, increases linearly. And thus, since 100kph is 2.5 times 40kph, braking time at 100kph is 2.5x that at 40kph.
The worst braking scenario is when the coefficient of friction is low--when the roads are wet, muddy, or iced up--and one is going downhill, with braking time and distance becoming greater as the inclination increases.
Hence, from the standpoint of safety the best thing a driver can do is to keep speeds low and/or to keep one's distance from other vehicles (and pedestrians) as large as practically possible. One can also apply the two-second rule. Although as weather and road conditions worsen this should be increased to three or four seconds.
Let
vi = initial velocity, m/s
vf = final velocity, m/s
v = average velocity, m/s
a = deceleration rate, m/s2
t = time to stop the vehicle, s
d = braking distance, m
μ = coefficient of friction, unitless
Ff = force of friction, kg·m/s2
Fn = normal force (force perpendicular to surface), kg·m/s2
Fg = force due gravity pulling the vehicle down a slope, kg·m/s2
m = mass, kg
g = gravitational acceleration, 9.8 m/s2
θ = angle of inclination (positive if vehicle going uphill, negative if going downhill)
Final velocity is given by the equation:
If vf = 0 then
Distance is given by:
Average velocity is:
Given vf = 0 and substituting we have:
Alternatively we can derive the distance formula using kinetic energy and work equations:
Equating work and energy we have:
Solving for d we obtain:
The force of friction is given by the following formula:
If the vehicle is on a level surface then normal force is just its weight. Therefore,
Since
then
Therefore,
Substituting the above into the distance and time equations we get:
Interesting to note that we can (at least in principle) determine the coefficient of friction by noting the velocity when the brakes are fully applied and time to bring the vehicle to a dead stop.
Now let's tackle the situation when the vehicle is braking on a slope.
When the vehicle is on an incline then a portion of the gravitational force acts to pull the vehicle down the slope. This force we denote as Fg and is derived via basic vector analysis. Refer to the free-body diagram. On the left of the diagram is an object on an incline with an angle of θ. Its weight is labeled as mg. Normal force Fn is the component of mg that is perpendicular to the incline. Fg is the component of mg that is parallel to the incline. To the right I've drawn a vector addition of the forces. Since this is a right triangle we can use the pertinent trigonometric functions: Sin θ = opposite side / hypotenuse. Cos θ = adjacent side / hypotenuse. Since the hypotenuse = mg we obtain the following:
An aside: Since the above are the legs of the right triangle it follows from the Pythagorean theorem that
When on a slope with the brakes engaged so that the vehicle is at a standstill Ff is the force that keeps the vehicle from slipping and sliding down and acts in the opposite direction as Fg which is pulling it down the incline. The net force holding the vehicle in place is therefore Ff - Fg. It stands to reason that when Fg becomes >= Ff then the vehicle--even with the brake pads fully gripping the brake discs and drums--will begin to slip and slide. We can calculate the angle of inclination at which this will occur:
Bear in mind that in this case we are using the static coefficient of friction rather than kinetic (or sliding) coefficient of friction since the vehicle is at rest with respect to the road.
When a vehicle is going downhill its braking distance will increase because a fraction of the gravitational force is acting to pull it down even when the brakes are applied. θ will be negative if going downhill, and so Fg will be negative. When going uphill part of gravitational force adds to the force of friction thereby decreasing braking distance.
The sum of forces acting on the vehicle parallel to its direction of motion is given by:
Since
Therefore,
Since
Substituting into our distance and time equations we obtain:
The above are exact equations in contrast to the approximate formula using road grade. The gradient is equal to the rise over run, or tangent of θ. The arctangent of the gradient = angle θ.
Reminder: when using the above equations θ should be negative when the vehicle is going downhill. Given -90° < θ < 0, sin θ is negative while cos θ is positive. Hence Fg is effectively subtracted from Ff. When going uphill and θ is positive then Ff is effectively increased by amount Fg. As anyone who's driven knows, it's harder to bring a vehicle to a stop when going downhill. And that it's easier to do so when going uphill than when on a level road.
Beware that the above distances and times do not take into account the driver's perception and reaction time--the time to perceive the need to stop and the time to actually to apply the brakes. This takes a minimum of around half a second for a driver who's alert and concentrating on the road, but may be much greater if the driver is drowsy, tired, intoxicated, on his cell phone, has poor eyesight, etc. or if visibility is poor among other possible factors beyond the driver's control.
The distance traveled by the vehicle during this time is simply
Here are a couple of online braking distance calculators which don't, however, have provisions for vehicles on an incline:
http://www.csgnetwork.com/stopdistcalc.html
http://forensicdynamics.com/stopping-distance-calculator
Tables of coefficients of friction:
http://www.engineeringtoolbox.com/friction-coefficients-d_778.html
http://www.roymech.co.uk/Useful_Tables/Tribology/co_of_frict.htm
Summary of the relevant data from the above tables:
| tire material | road type and condition | kinetic coefficient of friction |
|---|---|---|
| rubber | dry concrete | 0.6 - 0.85 |
| rubber | wet concrete | 0.45 - 0.75 |
| rubber | dry asphalt | 0.5 - 0.8 |
| rubber | wet asphalt | 0.25 - 0.75 |
A point worth mentioning: While the wheels are turning static coefficient of friction is operative because at the point of contact the tire is not sliding along the road. This is desirable because the static coefficient is higher than the kinetic coefficient of friction thus leading to decreased braking distance. Anti-lock brakes (ABS) prevent the wheels from locking even when the driver slams the brake pedal, therefore preventing the tires from skidding and sliding. However, the speed of the tire is lower than the vehicle's and so some slip occurs between tire and road. The static coefficient of friction cannot therefore be applied to vehicles even if they're equipped with ABS. For safety reasons it's best to be conservative and use the kinetic coefficient.
The take home lessons from the above formulas:
Braking distance varies with the square of velocity. Thus, doubling one's speed quadruples the distance. Increasing one's speed from 40kph to 100kph increases the braking distance by (100/40)2 = 6.25 times. Braking time, on the other hand, increases linearly. And thus, since 100kph is 2.5 times 40kph, braking time at 100kph is 2.5x that at 40kph.
The worst braking scenario is when the coefficient of friction is low--when the roads are wet, muddy, or iced up--and one is going downhill, with braking time and distance becoming greater as the inclination increases.
Hence, from the standpoint of safety the best thing a driver can do is to keep speeds low and/or to keep one's distance from other vehicles (and pedestrians) as large as practically possible. One can also apply the two-second rule. Although as weather and road conditions worsen this should be increased to three or four seconds.
Subscribe to:
Comments (Atom)