I'm currently designing and testing a 1-amp power supply based on the good old LM317 voltage regulator. I'd like it to be able to supply a voltage from its minimum of 1.25 V all the way to about 30 V. That's within its specs so no problem with that range. However, one problem is the power dissipation of the 317 which is given by:
\[
P_D = I_{VR} ( V_{IN} - V_{O})
\]
where
$P_D$ = power dissipation, in watts
$I_{VR}$ = current through the voltage regulator, mostly the load current, in amperes
$V_{IN}$ = input voltage, in volts
$V_{O}$ = output voltage, in volts
The higher the difference between input and output voltage the greater the power loss in the 317. If we use a single input voltage it would have to be at least 33VDC, more likely >35V to factor in capacitor ripple voltage. With an input of 35V and an output of, say, 5VDC headroom would be 30V. If the load were drawing 100mA it would dissipate 5V x 0.1A = 0.5W while the 317 would be wasting 30V x 0.1A = 3W! Without a heatsink and given the thermal resistance of a TO-220 package of around 65°C/W, the junction temperature would well exceed its 125°C maximum. Of course the 317 will probably shut down before reaching that temperature, or it might fry if the thermal overload protection circuitry somehow fails.Not that we wouldn't install a heatsink. It's indispensable for a 1000-mA supply since even with a constant headroom of 3V (minimum required), the regulator would still be dissipating 3W at a current draw of 1A. In fact my calculations show that on top a heat sink with a thermal resistance of <= 10°C/W, I'll still need a cooling fan given the headroom that my design has.
Heatsinking cannot be overemphasized in this design since with all else constant $V_{O}$ changes with junction temperature. If you check the graphs of any LM317 datasheet you will find that load regulation, adjustment current, and reference voltage are all temperature dependent. Therefore, keeping the 317 temperature as constant as possible is paramount for a good constant voltage output with a varying load.
So there are several reasons for limiting voltage headroom. And one way to do so is to use a multitap transformer and feed the 317 with a voltage that depends on its output. The greater the output voltage the higher the voltage we input to the regulator. A control circuit monitors $V_O$ and selects the appropriate transformer tap via electromagnetic relays.
Unfortunately, for this design I couldn't find a multiple tap transformer (with four or five outputs) whose maximum voltage output is 30 or so volts RMS. The best I could find is a 14-0-14 volt center-tapped, which is equivalent to a 0-14-28. With only two output voltages only one relay is necessary. The idea is to switch to 28VAC when $V_O$ rises above the middle value of around 12VDC and to switch back to 14VAC when it falls below this. A hysteresis band will be necessary to prevent relay "chatter" when crossing the switchover voltage.
In my first design I powered the $V_O$ monitoring circuit from the same transformer. But it turns out that because the secondary windings are not isolated from one another the voltages go haywire when the two taps are used simultaneously--by the 317 and the monitoring circuit. So I've had to use a second transformer, with 12VAC output, to drive the relay and power the ICs that check $V_{O}$.
The monitoring circuit consists simply of a comparator with hysteresis wired in using two positive feedback resistors. I've decided to switch the relay when $V_{O}$ is around 13VDC. I will definitely use $V_{O}$ = 12VDC so I don't want it switching at that level. And I can't change taps at a much higher voltage since there might not be enough headroom for the regulator when current draw goes above 500mA. So I've pegged the trip comparator trip voltage between 13 and 14VDC.
To determine the resistor values, upper and lower trip voltages, and the hysteresis band, I needed formulas. Textbooks have not been of any help. They do have the equations but they're for op amps using bipolar power supplies. I'm keeping to single-supply op amps and those equations simply don't work. I've tried them and results don't match with measured values. Luckily Microchip has the holy grail in their literature.
From the
Microchip MCP6541 datasheet we have the following equations to determine the trip voltages given positive feedback.
\[
V_{TLH} = V_{REF}\left ( 1 + \frac{ R_{F1}}{R_{F2}} \right ) - V_{OL} \left ( \frac{R_{F1}}{R_{F2}} \right)
\]
\[
V_{THL} = V_{REF}\left ( 1 + \frac{ R_{F1}}{R_{F2}} \right ) - V_{OH} \left ( \frac{R_{F1}}{R_{F2}} \right)
\]
where
$V_{TLH}$ = trip voltage when voltage at the noninverting input is going from low to high, in volts
$V_{THL}$ = trip voltage when voltage at the noninverting input is going from high to low, in volts
$V_{REF}$ = reference voltage, i.e., voltage at the comparator's inverting input, in volts
$V_{OL}$ = comparator low level output voltag, in volts
$V_{OH}$ = comparator high level output voltage, in volts
${R_{F1}}$, ${R_{F2}}$ = positive feedback resistances, in ohms
If output of the comparator is only very lightly loaded then $V_{OL}$ is only a few millivolts above ground. Moreover, ${R_{F1}}/{R_{F2}}$ is very small. Thus $V_{OL} ({R_{F1}}/{R_{F2}})$ is practically zero. $V_{TLH}$ then reduces to:
\[
V_{TLH} = V_{REF}\left ( 1 + \frac{ R_{F1}}{R_{F2}} \right )
\]
It follows then that
\[
V_{THL} = V_{TLH} - V_{OH} \left ( \frac{R_{F1}}{R_{F2}} \right)
\]
With a very lightly loaded comparator output, $V_{OH}$ is for all practical purposes equal to the comparator's supply voltage $V_{DD}$.
Upper and lower trip voltages in terms of $V_O$ are obtained as follows:
\[
V_{TLH}' = V_{TLH} \left ( \frac {R_{VD1}+R_{VD2}} {R_{VD2}} \right)
\]
\[
V_{THL}' = V_{THL} \left ( \frac {R_{VD1}+R_{VD2}} {R_{VD2}} \right)
\]
Referring to the schematic above, the comparator's reference voltage is derived from a voltage divider and computed as follows:
\[
V_{REF} = V_{DD} \left ( \frac {R_{REF2}}{R_{REF1} + R_{REF2}} \right)
\]
where
$R_{REF1}$ and $R_{REF2}$ are the voltage divider resistor values, in ohms
The LM317 output voltage $V_O$ is to be monitored by the comparator. But because this swings from 1.25 to around 30VDC, while the comparator maximum input voltage is $V_{DD}$ = 5VDC, we need to "step down" the voltage sensed by the comparator by using a voltage divider. $ R_{VD1}$ and $R_{VD2}$ are chosen such that when $V_O$ is at its maximum then voltage divider output is equal to the comparator $V_{DD}$. Voltage divider output is given by:
\[
V_O \left ( \frac {R_{VD2}}{R_{VD1}+R_{VD2}} \right)
\]
The presence of the feedback circuit in the comparator necessitates a low impedance source. The voltage divider formed by $R_{VD1}$ and $R_{VD2}$ does not meet this requirement. Hence a unity gain buffer is necessary.
I initially used a
MC33171 op amp for the comparator and a
LM310 voltage follower as the buffer. Instead of having two ICs I want to use a dual single supply op amp IC with a $V_{CC}$ of > 12VDC but unfortunately I don't have any at hand. But I do have tons of Microchip single, dual, and quad op amps. I picked the
MCP6282 for its rail-to-rail input and output and its good slew rate. $R_{VD1}$ and $R_{VD2}$ were chosen such that the voltage divider's maximum output is 5VDC.
Resistors, $V_{DD}$, and $V_{OH}$ of the breadboarded prototype were measured using a Fluke 8842A and their values were plugged into the equations above. $V_{TLH}'$ and $V_{THL}'$ were measured with the multimeter probes connected to $V_O$ and ground, and gradually turning the potentiometer. Theoretical and empirical results are within less than 0.25% of each other! That certainly blew my mind.
While designing this power supply I used an old malfunctioning ATX power supply 12VDC brushless motor cooling fan as a load since I could turn $V_O$ up and down and have some visual feedback on how it's affecting the load. And I could afford to ruin it should it burn up when I turned $V_O$ all the way up. Turns out choosing this fan was fortuitous because I discovered something totally unexpected. Without any load the comparator circuit worked fine and, depending on the values of the various resistors, there was some 1.5 to 2V ($V_O$) hysteresis band. But when the fan was powered hysteresis was lost and relay chatter was prominent when the trip voltage level was being crossed. I found out what was happening when I hooked up an oscilloscope to check $V_O$. It showed the fan was introducing positive and negative pulses (see oscilloscope screenshots below). And the comparator circuit was merely following what it's suppose to do--tripping (and being tripped up) when those pulses were present, as the difference between the peak positive and negative values exceeded the hysteresis band set by $R_{F1}$ and $R_{F2}$.
So I added a low pass filter section whose cutoff frequency can be computed as follows:
\[
f_c = \frac{1}{2\pi R_{LPF}C_{LPF}}
\]
where
$f_c$ = filter cutoff frequency, in hertz
$R_{LPF}$ = filter resistor value, in ohms
$C_{LPF}$ = filter capacitor value, in farads
This circuit filters out any transients occurring in $V_O$. With the LPF circuit in place oscilloscope reading of the unity gain buffer output was devoid of the noise pulses introduced by the fan.
I also used a new brushless DC fan as a load. Apparently even brand new fans also introduce spikes into $V_O$ although it seems their amplitude is not as high as those of the malfunctioning fan (see screenshots below). But the fans tested are made by different manufacturers so the noise they introduce may be manufacturer specific.
Given how the comparator and LPF circuits are working perfectly, I decided to lower the hysteresis band to a 500mV (measured at $V_O$), which translates to around 83mV at the comparator input. With resistor values (I used 5% resistors) provided in the schematic, actual measured upper trip voltage = 13.58V and lower trip voltage = 13.00V.
In the Rigol DS1102E oscilloscope screenshots below, channel 1 is set to AC coupling and bandwidth limit is on. $V_O$ is set to 12.50V as measured by the Fluke multimeter. All measurements are with respect to circuit ground.
Point of measurement: unity gain buffer output
Trigger: auto, @296mV
Vertical: 200mV/div
Horizontal: 5ms/div
The used, malfunctioning fan--a Power Logic brushless motor model PL80S12M rated at 12V 0.13A--is powered by $V_O$. There is
no low pass filter at the input of the voltage follower. Cursors are on and show that positive peak voltage = 384mVand peak negative voltage= -280mV. The comparator circuit sees these voltage spikes and when $V_O$ is at the trip setting the comparator output rapidly alternates between high and low (because the noise is greater than the hysteresis band) resulting in relay chatter.
Same screenshot as above but the cursors have been changed to measure time. As can be seen pulses occur every 6.7ms.
Point of measurement: unity gain buffer output
Trigger: single shot, 120mV
Vertical: 200mV/div
Horizontal: 2ms/div
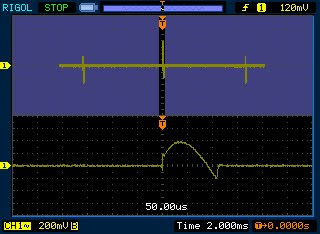
The lower waveform is a zoomed in display of the portion above that's between the purple bands. Time base for lower display = 50.00µs/div.
Same as above but zoomed in portion is that of the spike on the right. Time base is also 50µs/div
Point of measurement: unity gain buffer output
Trigger: auto, 0.00V
Vertical: 200mV/div
Horizontal: 5ms/div
The same fan is being powered by $V_O$, but now a first order low pass filter with a $f_c$ of 16Hz (as per schematic above) is connected to the input of the voltage follower. Voltage spikes have been completely eliminated and the comparator circuit performs flawlessly.
Point of measurement: $V_O$
Trigger: auto, @2.00V
Vertical: 1.00V/div
Horizontal: 20.00µs/div
This is the first type of pulse from the fan but measured at $V_O$. As can be seen it's the same as that output by the voltage follower without a low pass filter.
Point of measurement: $V_O$
Trigger: auto, @-1.68V
Vertical: 1.00V/div
Horizontal: 20.00µs/div
This is the second type of pulse but measured at $V_O$. As can be seen it's the same as that output by the voltage follower without a low pass filter.
Point of measurement: $V_O$
Trigger: auto, @1.08V
Vertical: 1.00V/div
Horizontal: 20.00µs/div
This is the only kind of pulse from a brand new ADDA Brushless DC motor model AD0812MS-A70GL rated at 12V 0.15A. Comparing the pulses, that from the Power Logic has a positive peak that reaches 2.1V while this new fan has a peak of only 1.2V. Negative peak is a bit harder to compare because the ADDA sometimes has negatives spikes that dip to around -2.0V.
The most crucial point in all this is that a low pass filter is essential for the $V_O$ monitoring circuit to work properly and reliably given various types of loads loads.
Backtracking a bit, filter capacitor sizing is important to make sure that ripple voltage at maximum rated current of the power supply is such that there is still enough headroom for the 317 to produce a regulated output. That is, at the comparator trip voltage (switching from lower to higher voltage transformer tap) and at the maximum voltage output of the 317 (~30VDC in this design) the following must hold true:
\[
V_{IN_{no\,load}}- V_{PPripple_{max\,load}} > V_{min\,headroom}
\]
where
$V_{IN_{no\,load}}$ = LM317 input voltage with no load at the output, in volts
$V_{PPripple_{max\,load}}$ = peak-to-peak ripple voltage at the input of the 317 with maximum load connected to its output, in volts
$V_{min\,headroom}$ = minimum headroom for the voltage regulator, in volts
Minimum headroom for the LM317 is around 2.5VDC. To allow enough leeway I peg it at 3V. This headroom requirement is the reason I chose a 14-0-14V over the more common 12-0-12V transformer. Tests with the latter yielded a poor headroom, its output being only 15VDC, rectified and filtered, even at no-load condition. That should in fact be 17.0VDC ($V_{RMS}\sqrt2 $). This problem may be manufacturer related, or I just got a bad batch. The 14-0-14V transformer (made by a different manufacturer) measured 19.6VDC (rectified, filtered, no-load) tapped at its 14VAC output, which is within 1% of the ideal value of 19.8V.
Assuming a ripple voltage that's triangular in waveform, the relation between peak-to-peak and RMS values of ripple voltage is given by:
\[
V_{PPripple} = V_{RMSripple}2\sqrt3
\]
For light loads the following approximation applies:
\[
V_{RMSripple} = \frac {I_{load}}{4\sqrt3 \,fC}
\]
where
$I_{load}$ = current draw of the load, in amperes
$f$ = mains/line frequency, in hertz
$C$ = capacitance of the filter capacitor, in farads
Peak-to-peak ripple is therefore,
\[
V_{PPripple} = \left ( \frac {I_{load}}{4\sqrt3 \,fC} \right ) 2\sqrt3
\]
\[
V_{PPripple} = \frac {I_{load}}{2fC}
\]
With a mains frequency of 60Hz the above simplifies to
\[
V_{PPripple} = \frac {I_{load}}{120C}
\]
In my design I set a limit of $V_{PPripple}$ = 1V. Plugging that into the formula yields a capacitor value of 8333µF. I will use either two 4700µF or one 10mF. Cap working voltage should be a minimum of 50V given the 40VAC peak of the transformer.
To adjust the 317's output I'm using is a
Bourns 3590S 5Kohm 10-turn precision potentiometer. A high quality pot is necessary to achieve good, reliable, stable resistance and, consequently, voltage output.
----
Note: LaTeX math code was embedded using
mathcache
----
References:
1. LM317 constant voltage reference design with protection diodes and bypass capacitors:
STMicroelectonics LM317 datasheet.
2. Equations for power dissipation of LM317 and heatsink requirements:
National Semiconductors LM317 datasheet.
3. Single-supply comparator hysteresis equations:
Microchip MCP6541 datasheet.
4. Equations for filter capacitor ripple voltage:
Electronics Devices and Circuit Theory, 4ed, Robert Boylestad & Louis Nashelsky, 1987, p.675 and Appendix B.;
Nuts and Volts, February 2004, p.11.